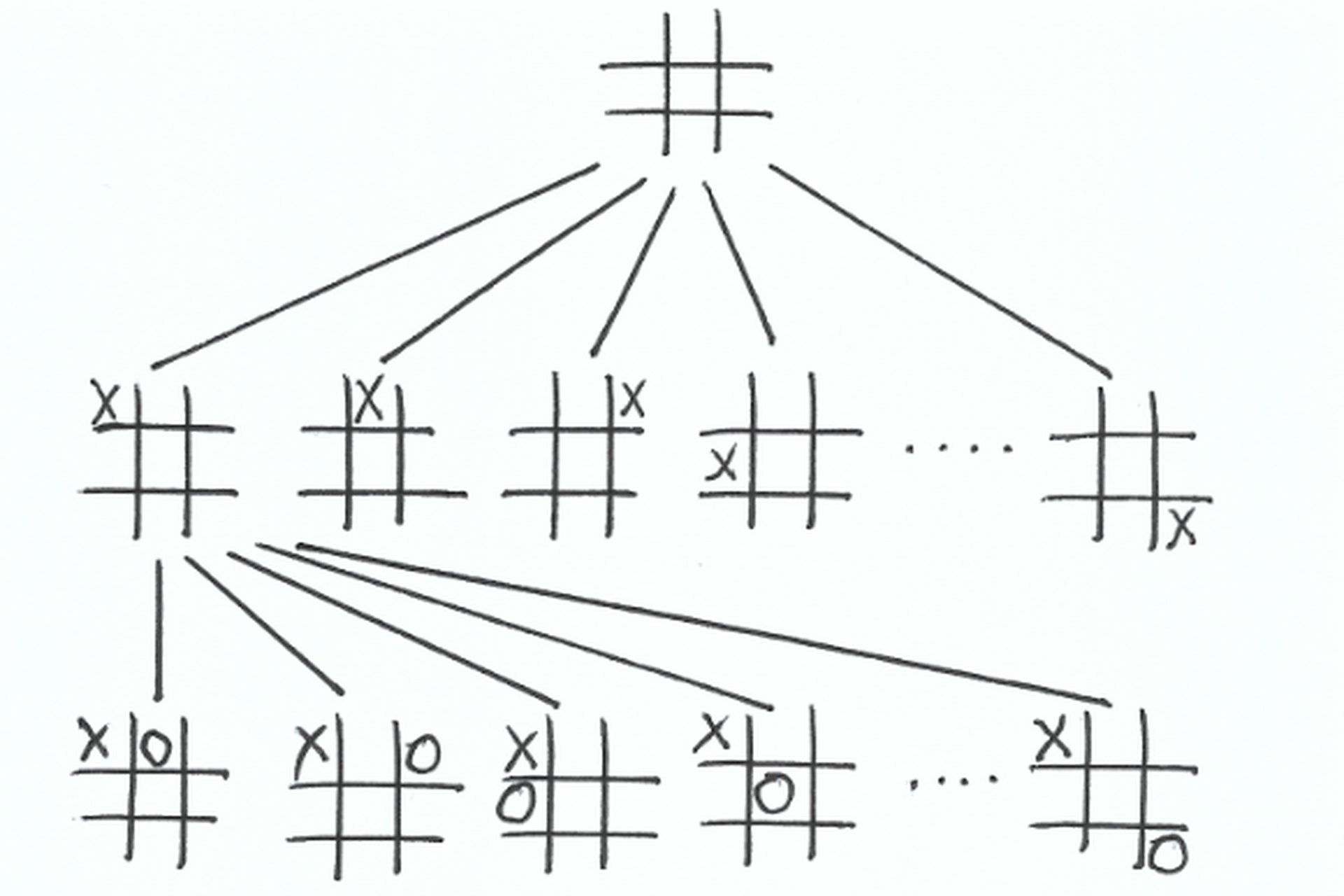
The internal game board is represented by a 3x3 matrix where digit “0” represents empty space. When user place mark “X”, digit “0” in matrix is replaced by digit “1” and digit “2” when CPU place mark “O”. Game is completed when all the spaces are marked unless any player wins before all the spaces are occupied. To keep track of game state we use state variable “step” and to keep track of which player turn is it state variable “turn” is used. If turn value is 0 it’s player turn and if it is 1 it’s CPU turn. Below is the code snippet for initialization.
class TicTacToe:
def __init__(self):
self.__game_board = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
self.__step = 0 # for tracking moves
self.__turn = 0 # if 0 -> player first and if 1 -> cpu first
self.__EMPTY_MARK = 0
self.__PLAYER_MARK = 1
self.__CPU_MARK = 2To show the external representation of game board. We loop through the rows and columns of the matrix and if particular position is marked as digit “0” is replaced by empty space. As stated above, player mark is represented by digit “1” so, if that particular position is equal to digit “1” in board, it is replaced by mark “X” same case for CPU mark as well mark “O” is placed if that position is occupied by digit “2”.
def __show_game_board(self):
print("\n\t\t+-----------+")
for i in range(3):
row_print = '\t\t|'
for j in range(3):
if self.__game_board[i][j] == self.__EMPTY_MARK:
row_print += ' |'
elif self.__game_board[i][j] == self.__PLAYER_MARK:
row_print += ' X |'
elif self.__game_board[i][j] == self.__CPU_MARK:
row_print += ' O |'
else:
print("something went wrong")
print(row_print)
print("\t\t+-----------+")We know that our internal game board representation is of 3x3 matrix and index starts from 0. So, to make input position convenient we assume index will start from 1 so that we can give marking position in the range [1,1] and [3,3] instead of [0,0] and [2,2] for start and last position in a matrix. But we update the internal game state of 3x3 matrix by substracting 1 from the provided position. We validate if the provided range is valid (i.e. in between [1,1] and [3,3]).
def __validate_coordinate(self, coordinate):
return (
coordinate[0] > 0 and
coordinate[1] > 0 and
coordinate[0] <= 3 and
coordinate[0] <= 3 and
self.__game_board[coordinate[0]-1][coordinate[1]-1] == self.__EMPTY_MARK # check if place is empty represented by 0
)To read position to place user mark we used the following function. We should given input position in the form of [num, num] and in valid range as stated above. If the range is not valid the program will prompt again for the input position until we provide valid empty position. The input is splitted into two digit to represent row and column position of matrix.
def __read_coordinate(self):
print("\n")
inp = input("Provide a valid and empty position to place your mark: ")
try:
inp_split = inp.split(',')
a = int(inp_split[0][1])
b = int(inp_split[1][0])
return [a, b]
except:
print("Invalid position!, Please enter a valid and empty position!")
self.__read_coordinate()
return NoneBelow is the code snippet to implement function to place player mark in the game board. The function will take a mark and coordinate (optional) parameters. The coordinate parameter is optional because only position is given by the player where as CPU will take position which will be suitable in order to win or draw the game by CPU. If coordinate is present, it is player move and if not it is CPU move. After either player played their move, the step is incremented by 1 and the turn is toggled. At the same time, after a player move, the win condition is checked.
def __place_mark(self, mark, coordinate=None):
if mark == self.__PLAYER_MARK:
self.__user_move(coordinate)
else:
self.__program_move()
self.__step += 1 # increment step
self.__turn = 1 if self.__turn == 0 else 0 # toggle turn
return self.__check_win(mark)The player move function will take coordinate as parameter and as mentioned above we decrement each (x,y) position by 1 and that position in matrix is replaced by 1(which is a user mark in the internal representation matrix).
def __user_move(self, coordinate):
self.__game_board[coordinate[0]-1][coordinate[1]-1] = 1The CPU move is a bit more complicated. If you have read the article about the tic tac toe game stategy, the optimal position is always has been a center position because by choosing a center position it will block the opponent chance to win from both diagonals as well as from central column and central row. So, the CPU will choose the center position if available. If central position is occupied, the CPU will look for the position to win. If it finds the position to win, it will place mark in that position. But if it unable to find wining position, it will place mark so as to prevent the opponent from winning. If the above contitions doesn’t meet it will place mark in any valid available position.
def __program_move(self):
# place mark at center position if empty
if self.__game_board[1][1] == self.__EMPTY_MARK:
self.__game_board[1][1] = self.__CPU_MARK
return
# check if it can win in next move
winning_coordinate = self.__next_winning_move(self.__CPU_MARK)
if winning_coordinate:
self.__game_board[winning_coordinate[0]][winning_coordinate[1]] = self.__CPU_MARK
return
# choose move that prevent oponent from winning
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == self.__EMPTY_MARK):
self.__game_board[i][j] = self.__CPU_MARK
# check if opponent win at this position
opp_winning_coordinate = self.__next_winning_move(self.__PLAYER_MARK)
self.__game_board[i][j] = self.__EMPTY_MARK
if opp_winning_coordinate:
self.__game_board[opp_winning_coordinate[0]][opp_winning_coordinate[1]] = self.__CPU_MARK
return
# choose available move
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == self.__EMPTY_MARK):
self.__game_board[i][j] = self.__CPU_MARK
returnThe below code snippet is for a function for CPU to check the next winning position. If the position is empty (represented by 0) the CPU will place mark and check for win condition. If it can win at this position it will again make this position as empty and return this position as coordinate. If it is unable to find win position, it will retrun None instead.
def __next_winning_move(self, mark):
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == self.__EMPTY_MARK):
self.__game_board[i][j] = mark
can_win = self.__check_win(mark)
self.__game_board[i][j] = self.__EMPTY_MARK
if can_win:
return [i, j]
return NoneThe function to check the win condition will take mark as a parameter. If either condition (i.e. any diagonal or any row or any column) that have same mark is the required condition to win the game. To check row or column win condition, we use rhe function check_row_column with optional parameter “row”. If row value is true that means it will check condition for row and if false it will check for column win condition.
To check diagonal we have check_diagonal_win with mark and reverse_game_board (optional). To use code resuability, we use same function to check the both diagnoal with optimal parameter reverse_game_board which is actually a reversed board of our game board so as to use same code for checking both diagonals.
def __check_win(self, mark):
reverse_game_board = list([row for row in reversed(self.__game_board)])
if(
self.__check_row_column(mark, row=True) or
self.__check_row_column(mark) or
self.__check_diagonal_win(mark) or
self.__check_diagonal_win(mark, reverse_game_board)
):
return mark
return FalseBelow is the code snippet to check row and column win condition. The idea is a bit tricky, initilizing the win_row_column variable to [0,0,0] is to run loop through the rows and columns of game matrix and check the values and increment these values by 1 if value at the particular row or column equals to the mark value.
Lets take an example, suppose we are checking the row win condition. The win_row_column = [0,0,0] initially, will denote the three rows of the board and if a particular rows have satisfied the win condition (i.e. a particular row contains same values) we increment value by 1 if a particular index position value equals to mark value.
Suppose the game state of the board is as follow
+-----------+
| X | | X |
+-----------+
| O | O | O |
+-----------+
| X | O | X |
+-----------+As we can see row win condition is satisfied in the second row. If we run loop through rows and columns for mark O (i.e. CPU mark and internal representation value of 2). First row doesn’t contain any CPU mark so first index value of win_row_column variable will be as it is (i.e. 0). When the loop continues for the second row and first column the internal value is 2 as it is represented by mark O so 1 is added to the 2nd index value of win_row_column (0+1=1). Again for the second column, the mark is again O so again value 1 is added in the same row index value of win_row_column (1+1=2). Same case for third column of second row of matrix. Where as for the third row it is only 1 because there is only one O mark in that row.
So, the final win_row_column variable value is equal to [0,3,1]. Now when we loop through it, if any value is equal to 3 means the win condition for row is satisfied so we returned value True otherwise we returned value False. Similar case of column win as well.
def __check_row_column(self, mark, row=False):
win_row_column = [0,0,0]
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == mark):
if row:
win_row_column[i] += 1
else:
win_row_column[j] += 1
for i in range(3):
if win_row_column[i] == 3:
return True
return FalseTo check diagonal we implement the following function. The optional parameter board is used to indicate if the contidion to be checked for the game board or for the reversed game board because if we reversed the board we can check the second diagonal with the same code which is used to check for the first diagonal. As we know for diagonal, the index value for row and column is same so if the diagonal position contain the value which is equal to the mark value we add 1 to the diag variable and if diag variable count is 3 the diagonal win condition is said to be satisfied and we return the True and False if value not equal to 3.
def __check_diagonal_win(self, mark, board=None):
diag = 0
if not board:
board = self.__game_board
for i in range(3):
for j in range(3):
if (i != j):
continue
if(board[i][j] == mark):
diag += 1
if diag == 3:
return True
return FalseBelow is the code snipet to implement the function to start the game. We run a while loop for condition “step value less than 9”. At first, the external representation of game board is shown then called a function to read position from user to place a mark “X” in the game board. We validate the position, if not valid user will be prompted again to enter correct valid position. Player will mark its position and check if he will win at this position otherwise its CPU turn to place mark. If either player wins or draw the final game board is displayed with the message of the result and final game board and then program will exit.
def start_game(self):
player_win = None
cpu_win = None
print("\n+-----------------------------------------------+")
print("\t\tTic Tac Toe")
print("\t+---------------------------+")
print("\n Valid empty position should be provided. ")
print(" Position should be in form of [num,num] ")
print(" and should be in the range of [1,3]. \n")
print(" Any other invalid input other than the ")
print(" provided range will again be prompted for ")
print(" input.")
print("\n+-----------------------------------------------+\n")
while(self.__step < 9):
self.__show_game_board()
coordinate = self.__read_coordinate()
try:
valid = self.__validate_coordinate(coordinate)
if not valid:
print("Invalid position!, Please enter a valid and empty position!")
coordinate = self.__read_coordinate()
except:
print("Invalid position!, Please enter a valid and empty position!")
coordinate = self.__read_coordinate()
player_win = self.__place_mark(self.__PLAYER_MARK, coordinate)
cpu_win = self.__place_mark(self.__CPU_MARK)
if player_win or cpu_win:
break
print("\n")
print("\t+---------------------------+")
print("\t\t Final Board!")
print("\t+---------------------------+")
self.__show_game_board()
if player_win == self.__PLAYER_MARK:
print("\t+---------------------------+")
print("\t\t Player Wins!")
print("\t+---------------------------+")
elif cpu_win == self.__CPU_MARK:
print("\t+---------------------------+")
print("\t\t CPU Wins!")
print("\t+---------------------------+")
else:
print("\t+---------------------------+")
print("\t\t Its a Tie!")
print("\t+---------------------------+")
sys.exit()The final code is given below
import sys
class TicTacToe:
def __init__(self):
self.__game_board = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
self.__step = 0 # for tracking moves
self.__turn = 0 # if 0 -> player first and if 1 -> cpu first
self.__EMPTY_MARK = 0
self.__PLAYER_MARK = 1
self.__CPU_MARK = 2
def __show_game_board(self):
print("\n\t\t+-----------+")
for i in range(3):
row_print = '\t\t|'
for j in range(3):
if self.__game_board[i][j] == self.__EMPTY_MARK:
row_print += ' |'
elif self.__game_board[i][j] == self.__PLAYER_MARK:
row_print += ' X |'
elif self.__game_board[i][j] == self.__CPU_MARK:
row_print += ' O |'
else:
print("something went wrong")
print(row_print)
print("\t\t+-----------+")
def __validate_coordinate(self, coordinate):
return (
coordinate[0] > 0 and
coordinate[1] > 0 and
coordinate[0] <= 3 and
coordinate[0] <= 3 and
self.__game_board[coordinate[0]-1][coordinate[1]-1] == self.__EMPTY_MARK # check if place is empty represented by 0
)
def __read_coordinate(self):
print("\n")
inp = input("Provide a valid and empty position to place your mark: ")
try:
inp_split = inp.split(',')
a = int(inp_split[0][1])
b = int(inp_split[1][0])
return [a, b]
except:
print("Invalid position!, Please enter a valid and empty position!")
self.__read_coordinate()
return None
def __place_mark(self, mark, coordinate=None):
if mark == self.__PLAYER_MARK:
self.__user_move(coordinate)
else:
self.__program_move()
self.__step += 1 # increment step
self.__turn = 1 if self.__turn == 0 else 0 # toggle turn
return self.__check_win(mark)
def __user_move(self, coordinate):
self.__game_board[coordinate[0]-1][coordinate[1]-1] = 1
def __program_move(self):
# place mark at center position if empty
if self.__game_board[1][1] == self.__EMPTY_MARK:
self.__game_board[1][1] = self.__CPU_MARK
return
# check if it can win in next move
winning_coordinate = self.__next_winning_move(self.__CPU_MARK)
if winning_coordinate:
self.__game_board[winning_coordinate[0]][winning_coordinate[1]] = self.__CPU_MARK
return
# choose move that prevent oponent from winning
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == self.__EMPTY_MARK):
self.__game_board[i][j] = self.__CPU_MARK
# check if opponent win at this position
opp_winning_coordinate = self.__next_winning_move(self.__PLAYER_MARK)
self.__game_board[i][j] = self.__EMPTY_MARK
if opp_winning_coordinate:
self.__game_board[opp_winning_coordinate[0]][opp_winning_coordinate[1]] = self.__CPU_MARK
return
# choose available move
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == self.__EMPTY_MARK):
self.__game_board[i][j] = self.__CPU_MARK
return
def __next_winning_move(self, mark):
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == self.__EMPTY_MARK):
self.__game_board[i][j] = mark
can_win = self.__check_win(mark)
self.__game_board[i][j] = self.__EMPTY_MARK
if can_win:
return [i, j]
return None
def __check_win(self, mark):
reverse_game_board = list([row for row in reversed(self.__game_board)])
if(
self.__check_row_column(mark, row=True) or
self.__check_row_column(mark) or
self.__check_diagonal_win(mark) or
self.__check_diagonal_win(mark, reverse_game_board)
):
return mark
return False
def __check_row_column(self, mark, row=False):
win_row_column = [0,0,0]
for i in range(3):
for j in range(3):
if(self.__game_board[i][j] == mark):
if row:
win_row_column[i] += 1
else:
win_row_column[j] += 1
for i in range(3):
if win_row_column[i] == 3:
return True
return False
def __check_diagonal_win(self, mark, board=None):
diag = 0
if not board:
board = self.__game_board
for i in range(3):
for j in range(3):
if (i != j):
continue
if(board[i][j] == mark):
diag += 1
if diag == 3:
return True
return False
def start_game(self):
player_win = None
cpu_win = None
print("\n+-----------------------------------------------+")
print("\t\tTic Tac Toe")
print("\t+---------------------------+")
print("\n Valid empty position should be provided. ")
print(" Position should be in form of [num,num] ")
print(" and should be in the range of [1,3]. \n")
print(" Any other invalid input other than the ")
print(" provided range will again be prompted for ")
print(" input.")
print("\n+-----------------------------------------------+\n")
while(self.__step < 9):
self.__show_game_board()
coordinate = self.__read_coordinate()
try:
valid = self.__validate_coordinate(coordinate)
if not valid:
print("Invalid position!, Please enter a valid and empty position!")
coordinate = self.__read_coordinate()
except:
print("Invalid position!, Please enter a valid and empty position!")
coordinate = self.__read_coordinate()
player_win = self.__place_mark(self.__PLAYER_MARK, coordinate)
cpu_win = self.__place_mark(self.__CPU_MARK)
if player_win or cpu_win:
break
print("\n")
print("\t+---------------------------+")
print("\t\t Final Board!")
print("\t+---------------------------+")
self.__show_game_board()
if player_win == self.__PLAYER_MARK:
print("\t+---------------------------+")
print("\t\t Player Wins!")
print("\t+---------------------------+")
elif cpu_win == self.__CPU_MARK:
print("\t+---------------------------+")
print("\t\t CPU Wins!")
print("\t+---------------------------+")
else:
print("\t+---------------------------+")
print("\t\t Its a Tie!")
print("\t+---------------------------+")
sys.exit()
if __name__ == '__main__':
ttt = TicTacToe()
ttt.start_game()